图片加载可能有点慢，请跳过题面先看题解，谢谢

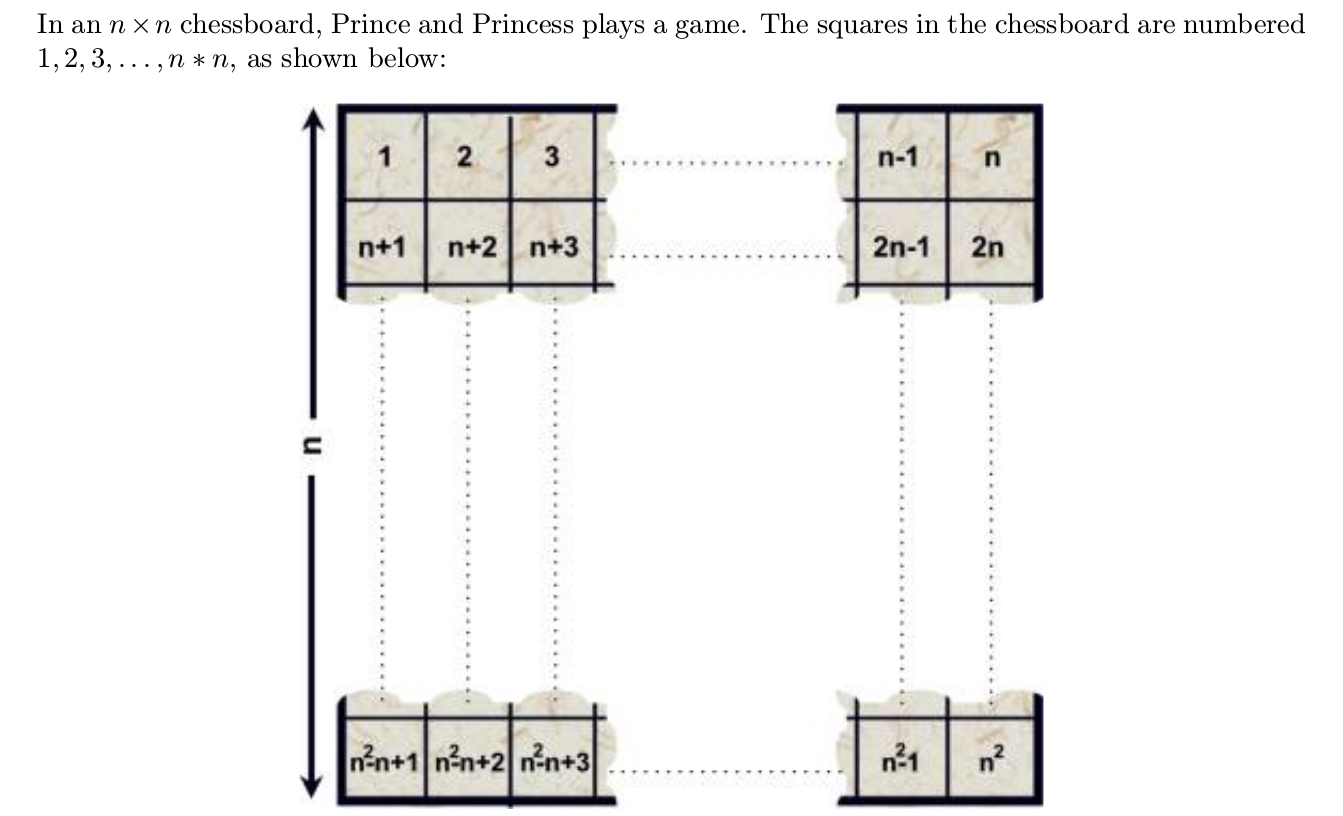
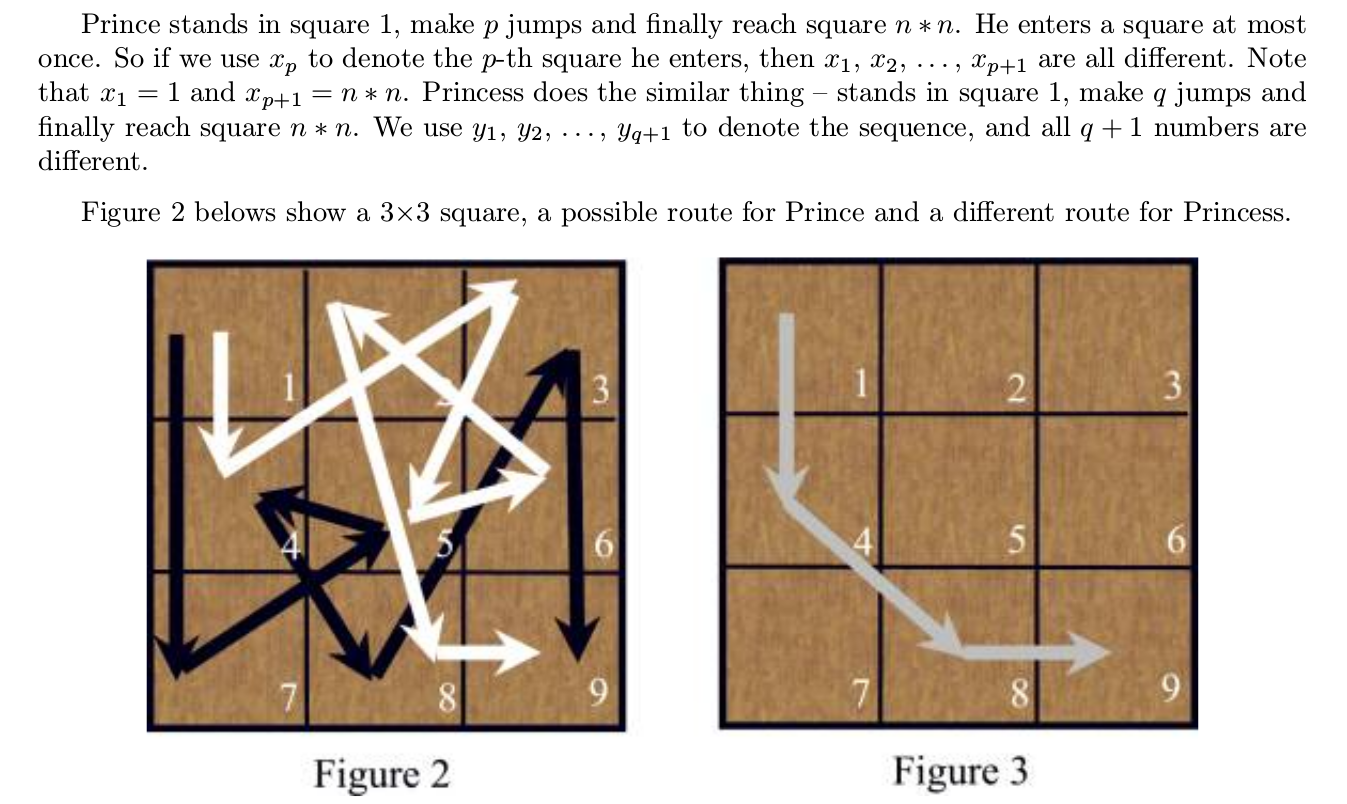
这道题。。。

还是要点思维的。。。

第一眼看是个最长公共子序列，但是， \(N\le 62500\) ，并不能 \(O(n^2)\) 求

$

$

这道题有个很好的性质，每个序列中的元素互不相同

也就是说，在一个序列中，每一个数字都有一个唯一的位置

这有什么用？

$

$

我们进行这样一个操作，把 \(b\) 序列中的数字换成该数字在 \(a\) 序列中出现的位置，那么问题就变成了一个求 \(b\) 序列的 \(LCS\) 的问题了

这样我们就可以在 \(O(nlogn)\) 的复杂度下解决这个问题

再吐槽一下。。。

做这道题目，思考 \(10min\) ，代码调试 \(2h\) ，震惊，原因竟是？

看下这个语句：

我写的： \(a[++k]=max(a[k],x)\)

AC程序： \(a[k+1]=max(a[k+1],x)\)，或者 \(a[k]=max(a[++k],x)\)

//made by Hero_of_Someone#include
    
     #include
     
      #include
      
       #include
       
        #define il inline#define RG registerusing namespace std;il int gi(){ RG int x=0,q=1; RG char ch=getchar(); while( ( ch<'0' || ch>'9' ) && ch!='-' ) ch=getchar();  if( ch=='-' ) q=-1,ch=getchar(); while(ch>='0' && ch<='9') x=x*10+ch-48,ch=getchar(); return q*x; }int T,t,N,n,m,cnt;int a[100010],b[100010],id[100010];il void init(){   N=gi(),n=gi()+1,m=gi()+1;   memset(id,0,sizeof(id)); cnt=0;   for(RG int i=1;i<=n;i++) a[i]=gi(),id[a[i]]=i;   for(RG int i=1;i<=m;i++){ b[i]=gi();      if(id[b[i]]) b[++cnt]=id[b[i]];   }}il void work(){   n=cnt,cnt=0;   memset(a,0x3f3f3f3f,sizeof(a));   for(RG int i=1;i<=n;i++){      RG int x=b[i];      RG int l=1,r=cnt,k=0;      while(l<=r){         RG int mid=(l+r)>>1;         if(a[mid]>x) r=mid-1;         else l=mid+1,k=mid;      }      if(k==cnt) a[++cnt]=x;      else a[k]=min(a[++k],x);   }   printf("Case %d: %d\n",t,cnt);}int main(){ T=gi(); for(t=1;t<=T;t++){ init(); work(); } return 0; }